Арифметическая прогрессия
Материал из Википедии — свободной энциклопедии
Арифмети́ческая прогре́ссия (алгебраическая) — числовая последовательность вида
 ,
,
то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа  (шага, или разности прогрессии):
(шага, или разности прогрессии):
 (шага, или разности прогрессии):
(шага, или разности прогрессии):
Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:
Арифметическая прогрессия является монотонной последовательностью . При 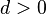 она является возрастающей, а при
она является возрастающей, а при  — убывающей. Если
— убывающей. Если 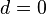 , то последовательность будет стационарной. Эти утверждения следуют из соотношения
, то последовательность будет стационарной. Эти утверждения следуют из соотношения  для членов арифметической прогрессии.
для членов арифметической прогрессии.
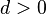 она является возрастающей, а при
она является возрастающей, а при  — убывающей. Если
— убывающей. Если 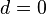 , то последовательность будет стационарной. Эти утверждения следуют из соотношения
, то последовательность будет стационарной. Эти утверждения следуют из соотношения  для членов арифметической прогрессии.
для членов арифметической прогрессии.Свойства
Общий член арифметической прогрессии
Член арифметической прогрессии с номером  может быть найден по формуле
может быть найден по формуле
 , где
, где  — первый член прогрессии,
— первый член прогрессии,  — её разность.
— её разность.
 может быть найден по формуле
может быть найден по формуле , где
, где  — первый член прогрессии,
— первый член прогрессии,  — её разность.
— её разность.| Доказательство |
|---|
Пользуясь соотношением  выписываем последовательно несколько членов прогрессии: выписываем последовательно несколько членов прогрессии:   
Заметив закономерность, делаем предположение, что
 . С помощью математической индукции покажем, что предположение верно для всех . С помощью математической индукции покажем, что предположение верно для всех  : :
База индукции
 : : — утверждение истинно. — утверждение истинно.
Переход индукции:
Пусть наше утверждение верно при
 , то есть , то есть  . Докажем истинность утверждения при . Докажем истинность утверждения при  : :
Итак, утверждение верно и при
 . Это значит, что . Это значит, что  для всех для всех  . . |
Характеристическое свойство арифметической прогрессии
Последовательность  есть арифметическая прогрессия
есть арифметическая прогрессия  для любого её элемента выполняется условие
для любого её элемента выполняется условие  .
.
 есть арифметическая прогрессия
есть арифметическая прогрессия  для любого её элемента выполняется условие
для любого её элемента выполняется условие  .
.| Доказательство |
|---|
| Необходимость:
Поскольку
 — арифметическая прогрессия, то для — арифметическая прогрессия, то для 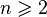 выполняются соотношения: выполняются соотношения:  . .
Сложив эти равенства и разделив обе части на 2, получим
 . .
Достаточность:
Имеем, что для каждого элемента последовательности, начиная со второго, выполняется
 . Следует показать, что эта последовательность есть арифметическая прогрессия. Преобразуем эту формулу к виду . Следует показать, что эта последовательность есть арифметическая прогрессия. Преобразуем эту формулу к виду  . Поскольку соотношения верны при всех . Поскольку соотношения верны при всех 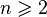 , с помощью математической индукции покажем, что , с помощью математической индукции покажем, что  . .
База индукции
 : : — утверждение истинно. — утверждение истинно.
Переход индукции:
Пусть наше утверждение верно при
 , то есть , то есть  . Докажем истинность утверждения при . Докажем истинность утверждения при  : :
Но по предположению индукции следует, что
 . Получаем, что . Получаем, что 
Итак, утверждение верно и при
 . Это значит, что . Это значит, что  . .
Обозначим эти разности через
 . Итак, . Итак,  , а отсюда имеем , а отсюда имеем  для для  . Поскольку для членов последовательности . Поскольку для членов последовательности  выполняется соотношение выполняется соотношение  , то это есть арифметическая прогрессия. , то это есть арифметическая прогрессия. |
Сумма первых  членов арифметической прогрессии
членов арифметической прогрессии
Сумма первых  членов арифметической прогрессии
членов арифметической прогрессии  может быть найдена по формулам
может быть найдена по формулам
 , где
, где  — первый член прогрессии,
— первый член прогрессии,  — член с номером
— член с номером  ,
,  — количество суммируемых членов.
— количество суммируемых членов. — формула Алпеева , где
— формула Алпеева , где  — первый член прогрессии,
— первый член прогрессии, 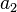 — второй член прогрессии
— второй член прогрессии  — член с номером
— член с номером  .
. , где
, где  — первый член прогрессии,
— первый член прогрессии,  — разность прогрессии,
— разность прогрессии,  — количество суммируемых членов.
— количество суммируемых членов.
 членов арифметической прогрессии
членов арифметической прогрессии  может быть найдена по формулам
может быть найдена по формулам , где
, где  — первый член прогрессии,
— первый член прогрессии,  — член с номером
— член с номером  ,
,  — количество суммируемых членов.
— количество суммируемых членов. — формула Алпеева , где
— формула Алпеева , где  — первый член прогрессии,
— первый член прогрессии, 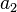 — второй член прогрессии
— второй член прогрессии  — член с номером
— член с номером  .
. , где
, где  — первый член прогрессии,
— первый член прогрессии,  — разность прогрессии,
— разность прогрессии,  — количество суммируемых членов.
— количество суммируемых членов.| Доказательство |
|---|
Запишем сумму двумя способами:  — та же сумма, только слагаемые идут в обратном порядке. — та же сумма, только слагаемые идут в обратном порядке.
Теперь прибавим оба равенства, последовательно прибавляя в правой части слагаемые, которые стоят на одной вертикали:

Покажем, что все слагаемые (все скобки) полученной суммы равны между собой. В общем виде каждое слагаемое можно подать в виде
 . Воспользуемся формулой общего члена арифметической прогрессии: . Воспользуемся формулой общего члена арифметической прогрессии:
Получили, что каждое слагаемое не зависит от
 и равно и равно  . В частности, . В частности,  . Поскольку таких слагаемых . Поскольку таких слагаемых  , то , то
Третья формула для суммы получается подстановкой
 вместо вместо  . Что и так непосредственно следует из выражения для общего члена. . Что и так непосредственно следует из выражения для общего члена.
Замечание:
Вместо
 в первой формуле для суммы можно взять любое из других слагаемых в первой формуле для суммы можно взять любое из других слагаемых  , так как они все равны между собой. , так как они все равны между собой. |
Сходимость арифметической прогрессии
Арифметическая прогрессия  расходится при
расходится при  и сходится при
и сходится при 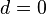 . Причём
. Причём

 расходится при
расходится при  и сходится при
и сходится при 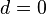 . Причём
. Причём
| Доказательство |
|---|
Записав выражение для общего члена и исследуя предел  , получаем искомый результат. , получаем искомый результат. |
Связь между арифметической и геометрической прогрессиями
Пусть  — арифметическая прогрессия с разностью
— арифметическая прогрессия с разностью  и число
и число  . Тогда последовательность вида
. Тогда последовательность вида  есть геометрическая прогрессия со знаменателем
есть геометрическая прогрессия со знаменателем  .
.
 — арифметическая прогрессия с разностью
— арифметическая прогрессия с разностью  и число
и число  . Тогда последовательность вида
. Тогда последовательность вида  есть геометрическая прогрессия со знаменателем
есть геометрическая прогрессия со знаменателем  .
.| [скрыть]Доказательство |
|---|
| Проверим характеристическое свойство для образованной геометрической прогрессии:
Воспользуемся выражением для общего члена арифметической прогрессии:
Итак, поскольку характеристическое свойство выполняется, то
 — геометрическая прогрессия. Её знаменатель можно найти, например, из соотношения — геометрическая прогрессия. Её знаменатель можно найти, например, из соотношения  . . |
Арифметические прогрессии высших порядков
Арифметической прогрессией второго порядка называется такая последовательность чисел, что последовательность их разностей сама образует простую арифметическую прогрессию. Примером может служить последовательность квадратов натуральных чисел:
- 0, 1, 4, 9, 16, 25, 36…,
разности которых образуют простую арифметическую прогрессию с разностью 2:
- 1, 3, 5, 7, 9, 11…
Аналогично определяются и прогрессии более высоких порядков. В частности, последовательность n-ных степеней образует арифметическую прогрессиюn-го порядка.
Если ![\left [ a_{i} \right ]_{1}^{n}](https://upload.wikimedia.org/math/9/7/5/975ba699f345b49682600b88cce3f4be.png) — арифметическая прогрессия порядка
— арифметическая прогрессия порядка  , то существует многочлен
, то существует многочлен  , такой, что для всех
, такой, что для всех  выполняется равенство
выполняется равенство  [1]
[1]
![\left [ a_{i} \right ]_{1}^{n}](https://upload.wikimedia.org/math/9/7/5/975ba699f345b49682600b88cce3f4be.png) — арифметическая прогрессия порядка
— арифметическая прогрессия порядка  , то существует многочлен
, то существует многочлен  , такой, что для всех
, такой, что для всех  выполняется равенство
выполняется равенство  [1]
[1]Примеры
- Натуральный ряд
 — это арифметическая прогрессия, в которой первый член
— это арифметическая прогрессия, в которой первый член  , а разность
, а разность  .
.
 — первые 5 членов арифметической прогрессии, в которой
— первые 5 членов арифметической прогрессии, в которой  и
и  .
.- Если все элементы некоторой последовательности равны между собой и равны некоторому числу
 , то это есть арифметическая прогрессия, в которой
, то это есть арифметическая прогрессия, в которой  и
и 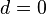 . В частности,
. В частности,  есть арифметическая прогрессия с разностью
есть арифметическая прогрессия с разностью 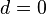 .
.
- Сумма первых
 натуральных чисел выражается формулой
натуральных чисел выражается формулой
 .
.
 — это арифметическая прогрессия, в которой первый член
— это арифметическая прогрессия, в которой первый член  , а разность
, а разность  .
. — первые 5 членов арифметической прогрессии, в которой
— первые 5 членов арифметической прогрессии, в которой  и
и  .
. , то это есть арифметическая прогрессия, в которой
, то это есть арифметическая прогрессия, в которой  и
и 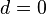 . В частности,
. В частности,  есть арифметическая прогрессия с разностью
есть арифметическая прогрессия с разностью 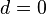 .
. натуральных чисел выражается формулой
натуральных чисел выражается формулой .
.Занимательная история
Согласно легенде, школьный учитель математики юного Гаусса, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат: 5050. Действительно, легко видеть, что решение сводится к формуле

то есть к формуле суммы первых  чисел натурального ряда.
чисел натурального ряда.

 чисел натурального ряда.
чисел натурального ряда.Геометрическая прогрессия
Геометри́ческая прогре́ссия — последовательность чисел  (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число
(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число 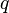 (знаменатель прогрессии), где
(знаменатель прогрессии), где  ,
, 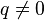 :
: 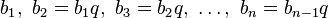 .
.
Геометри́ческая прогре́ссия — последовательность чисел  (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число
(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число 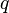 (знаменатель прогрессии), где
(знаменатель прогрессии), где  ,
, 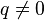 :
: 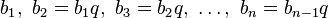 .
.
 (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число
(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число 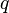 (знаменатель прогрессии), где
(знаменатель прогрессии), где  ,
, 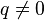 :
: 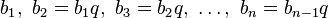 .
.
Описание
Любой член геометрической прогрессии может быть вычислен по формуле:
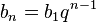
Если  и
и  , прогрессия является возрастающей последовательностью, если
, прогрессия является возрастающей последовательностью, если  , — убывающей последовательностью, а при
, — убывающей последовательностью, а при  —знакочередующейся.
Своё название прогрессия получила по своему характеристическому свойству:
—знакочередующейся.
Своё название прогрессия получила по своему характеристическому свойству:

то есть каждый член равен среднему геометрическому его соседей.
Любой член геометрической прогрессии может быть вычислен по формуле:
Если  и
и  , прогрессия является возрастающей последовательностью, если
, прогрессия является возрастающей последовательностью, если  , — убывающей последовательностью, а при
, — убывающей последовательностью, а при  —знакочередующейся.
—знакочередующейся.
 и
и  , прогрессия является возрастающей последовательностью, если
, прогрессия является возрастающей последовательностью, если  , — убывающей последовательностью, а при
, — убывающей последовательностью, а при  —знакочередующейся.
—знакочередующейся.
Своё название прогрессия получила по своему характеристическому свойству:
то есть каждый член равен среднему геометрическому его соседей.
Примеры
Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата.
- Последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
- 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — прогрессия со знаменателем 2 из тринадцати членов.
- 50; −25; 12,5; −6,25; 3,125; … — бесконечно убывающая прогрессия со знаменателем -½.
 — геометрическая прогрессия со знаменателем 1 (и арифметическая прогрессия с шагом 0).
— геометрическая прогрессия со знаменателем 1 (и арифметическая прогрессия с шагом 0).
Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата.
- Последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
- 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — прогрессия со знаменателем 2 из тринадцати членов.
- 50; −25; 12,5; −6,25; 3,125; … — бесконечно убывающая прогрессия со знаменателем -½.
 — геометрическая прогрессия со знаменателем 1 (и арифметическая прогрессия с шагом 0).
— геометрическая прогрессия со знаменателем 1 (и арифметическая прогрессия с шагом 0).
Свойства
Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.
 , если
, если  .
.
- Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
 .
.
- Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:
 .
.
- Сумма
 первых членов геометрической прогрессии:
первых членов геометрической прогрессии:

- Если
 , то
, то  при
при  , и
, и
 при
при  .
.
 , если
, если  .
.
- Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
 .
.
- Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:
 .
.
- Сумма
 первых членов геометрической прогрессии:
первых членов геометрической прогрессии:
- Если
 , то
, то  при
при  , и
, и
 при
при  .
.




 Формула общего члена арифметической прогрессии:
Формула общего члена арифметической прогрессии: 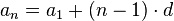 .
. ,
, .
.
 Раскроем произведение
Раскроем произведение  :
:  Выражение
Выражение  представляет собой
представляет собой 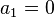 и шагом 1. Сумма первых n членов прогрессии равна
и шагом 1. Сумма первых n членов прогрессии равна  . Откуда
. Откуда 


 или
или .
.


Комментариев нет:
Отправить комментарий